Summer SAVY, Session 5 Day 3, “The Origins of Math: Discovery or Invention?” (5th-6th)
We started the day with cognitive puzzles, which have been slowly increasing in difficulty, going from a mix of hard to challenging. Our students have been rising to the occasion using collaborative work, well-formulated questions to the teacher, and simple perseverance. For every solved puzzle, a paper construction was taking flight across the room. We are definitely ready to host a paper airplane convention! I would like to think that our collectively acquired knowledge on the origins of math is experiencing an evolution not unlike the one I am observing in the quality of flight paths of the little planes zooming about the classroom ceiling. The flights are smooth; pilots perform multiple turns and twirls, survive the turbulence, and come back to base for more structural improvements. The kids are rocking the socks off this curriculum!
As we were learning how the human brain reacts to mathematical problems vs. language tasks, we held a classroom discussion to answer the following questions: Is math a part of our brain? What evidence do we have to support our opinions on this matter? Can this evidence be used to prove the opposite? Do babies have a sense of quantity? (We watched an experiment that seemed to prove that babies just a few months old have a sense of quantity.) Do pets? Some students shared fun and heartwarming examples of how their pets and much younger siblings (babies) definitely have a sense of quantity. At the same time, solid arguments were made by a few students that these observations could be a result of our desire to see math in every situation, and an equally valid explanation is possible without mathematical sense being an explanation.
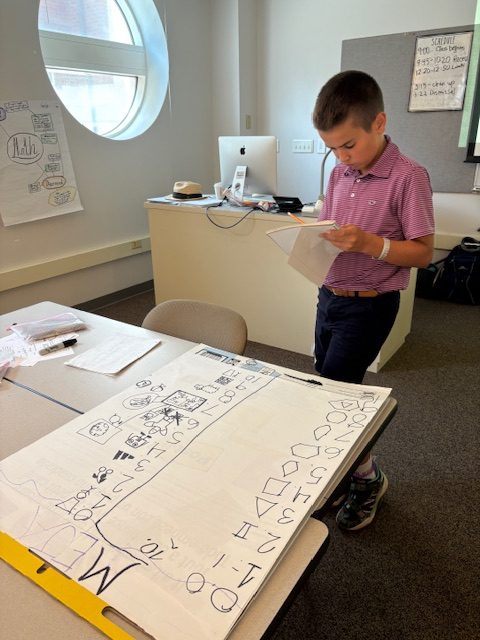
Before lunch, students worked on their Number Systems projects. Each group sent one travelling-student-researcher to explore other groups’ Number Systems. There were special limitations placed on these visits. Traveling researchers were allowed to ask questions only during one of the visits and silently observe during the other. Upon their return, researchers briefed the group members, and the entire group was only allowed to potentially borrow one idea from other mathematical civilizations (other groups). I cannot wait to share photos of our completed Number Systems in our Friday blog because it is going to be epic!
After lunch, we followed Marcus du Sautoy to Ancient China, making interesting connections between how ancient Chinese solved and balanced equations to the balancing equations puzzles we have been working on since Monday.
Questions of the Day: What is your group’s symbol for 100 in a visual number system? In a cultural one? Have you finalized addition and subtraction operations?
Bonus Question: If you stole a second piece of candy from a younger sister, is she crying because she has not met the sugar ration for the day or because she knows she now has to express her sugar intake as 2C – C vs. 2C? (Unless she gives chase, bites you, wins her candy back, and steals your lunch money.) In which case, science is powerless in writing out this equation. (Still, give it a try, and show it to me in the morning.)
