Hello SAVY Families!
We had another fantastic day at SAVY Summer 2025 Session Five: Encounters with Measurement. Once again, the SAVY Mathematicians outdid themselves in their work today, and I know that each of them walked away with a better understanding of mathematical concepts such as perimeter, area, and the distributive property of multiplication.
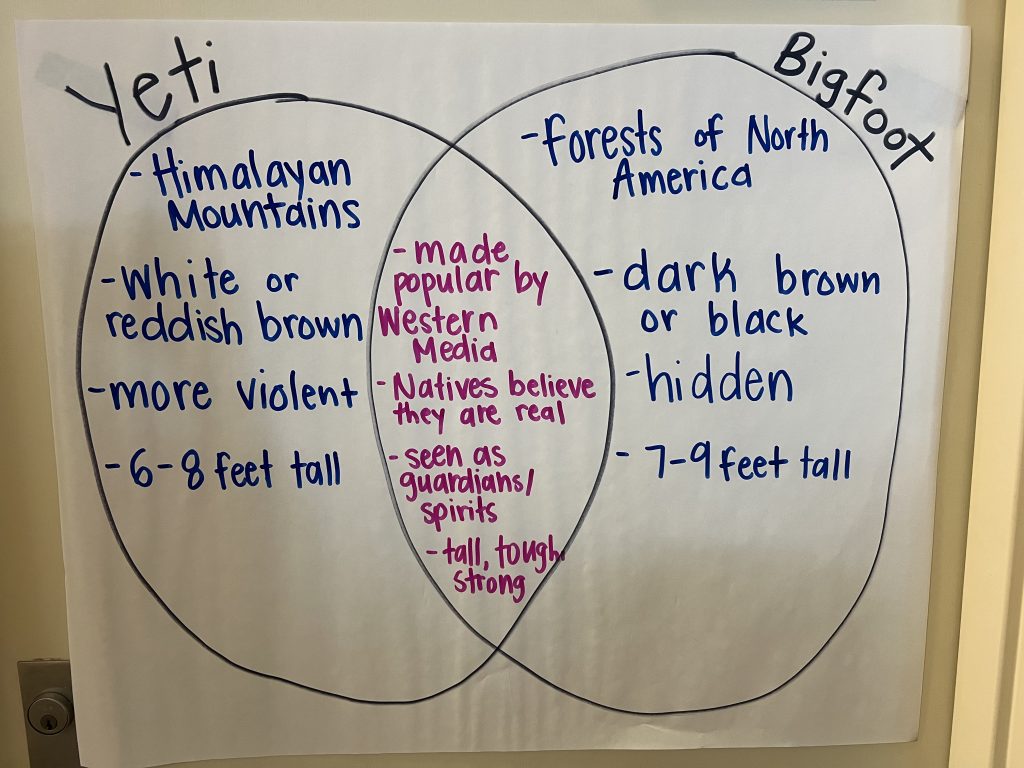
To start our class, we reviewed class concepts from yesterday and answered any lingering questions that the mathematicians had about measurement, accuracy, and estimation. Many mathematicians were eager to share the measurements they took of their family members last night. To get excited about our learning, we watched a video outlining the similarities and differences between the Himalayan yeti and the North American Bigfoot. We created a Venn Diagram to show what is the same about these two creatures and what is different about these two creatures. Next, we jumped into the first concept of the day: perimeter. Our mathematicians discovered that the perimeter is defined as the distance around the outside of a figure. Students found the perimeter of a rectangle and were challenged to draw additional rectangles with the same perimeter. Then, a big discovery was made! Students recognized that even with the same perimeter, some rectangles that were drawn had a different amount of space inside the figure. This led to our next concept: area.
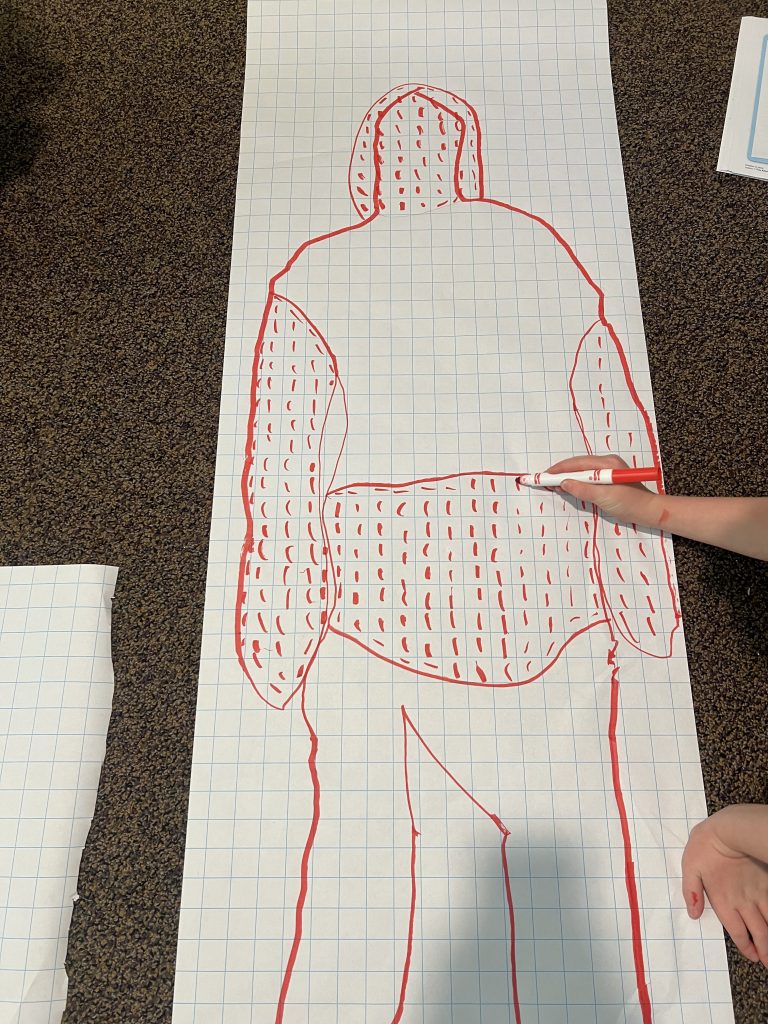
Area is defined as the region inside the boundaries of a two-dimensional closed figure. Area is measured in square units. We had a great discussion about why units are defined as “square” units, and students grasped this concept quickly. We started by drawing a fried egg, and using square centimeters to figure out the approximate area of the outline of the fried egg. We discussed how to find an area when not all of the squares are fully covered by the egg, and how this poses a challenge to mathematicians like us. Next, we upped the scale. Students had their bodies traced on a square inch grid paper. On this paper, mathematicians estimated the area of different body parts, and then they added the area of the body parts together to find the total area, in square inches, of the outline of a mathematician’s body. We know that we cannot find the area of an actual body because our bodies are three-dimensional; however, we can trace our body and find the outline of a two-dimensional tracing. This was definitely a favorite activity of the day!
To end our discussion on area, we came back to finding the area of regular rectangles. Students learned about the distributive property of multiplication and how that property can be used to partition large rectangles to find their area. We started small, finding the areas of 2 ft x 3 ft rectangles, and ended our day by finding the area of a 9 ft x 19 ft rectangle. Students were eager to share their process and their thinking, and it was truly inspiring to see how many different strategies the mathematicians were able to come up with! Finally, the mathematicians had to take a figure made up of different rectangles, partition the figure into rectangles, and then find the area of each of these rectangles to find the area of the whole figure.
Questions to ask your mathematician this evening:
- What is the same about Yeti and Bigfoot? What is different?
- What is perimeter? How do you find the perimeter of a shape? What units do you use?
- What is area? How do you find the area of a shape? What units do you use?
- Can two shapes have the same perimeter and different areas? Can two shapes have the same area and different perimeters?
- How does the area of the body outline of a first grader compare to the area of the body outline of an adult? How do you know?
I look forward to continuing our learning together the rest of this week. Have a great evening!